Te recomiendo estudiar estos temas antes de comenzar esta lección:
- Descomponer un número en sus factores primos
Zona de descargas:
Profundiza el contenido con este video:
Desarrollo:
Ordenamos el trinomio de forma descendente
Abrimos dos paréntesis
En ambos paréntesis se coloca como primer término la raíz cuadrada del primer término del trinomio.
El segundo signo del trinomio será el signo que separa al binomio del primer paréntesis.
Se multiplican los signos del trinomio y el resultado será el signo que separe al binomio del segundo paréntesis.
Se descompone en sus factores primos el último término del trinomio y se buscan dos números que cumplan las siguientes condiciones:
Si los signos son iguales, se buscan dos números cuya suma sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
Si los signos son diferentes, se buscan dos números cuya diferencia sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio
El número más grande se coloca como segundo término del binomio del primer paréntesis y el número más pequeño encontrado se coloca como segundo término del binomio del segundo paréntesis.
Ejemplos variados:
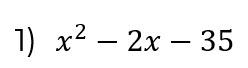
Abrimos dos paréntesis y a ambos le colocamos la raíz cuadrada del primer término:
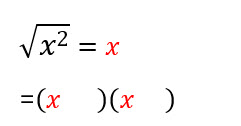
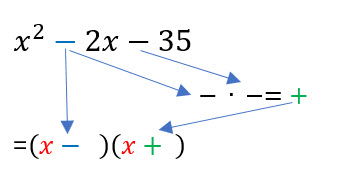
El segundo signo del trinomio será el signo que separa al binomio del primer paréntesis. Además se multiplican los signos del trinomio y el resultado será el signo que separe al binomio del segundo paréntesis.
Se descompone en sus factores primos el último término del trinomio
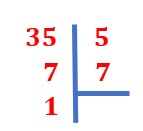
Como los signos son diferentes, se buscan dos números cuya diferencia sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio, en este caso son el 7 y el 5

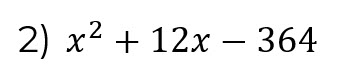
Abrimos dos paréntesis y a ambos le colocamos la raíz cuadrada del primer término:
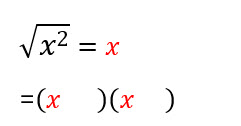
El segundo signo del trinomio será el signo que separa al binomio del primer paréntesis. Además se multiplican los signos del trinomio y el resultado será el signo que separe al binomio del segundo paréntesis.
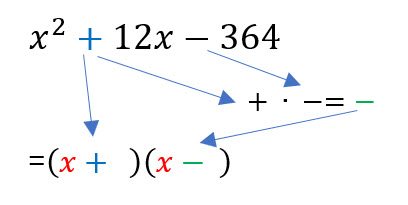
Se descompone en sus factores primos el último término del trinomio
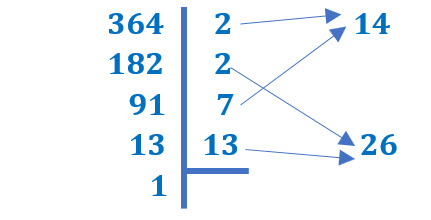
Como los signos son diferentes, se buscan dos números cuya diferencia sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio, en este caso son el 26 y el 14

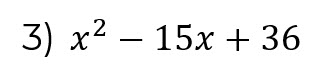
Abrimos dos paréntesis y a ambos le colocamos la raíz cuadrada del primer término:
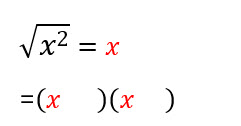
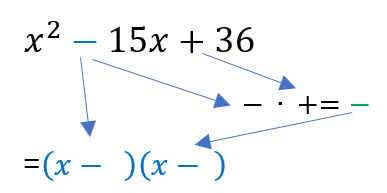
El segundo signo del trinomio será el signo que separa al binomio del primer paréntesis. Además se multiplican los signos del trinomio y el resultado será el signo que separe al binomio del segundo paréntesis.
Se descompone en sus factores primos el último término del trinomio
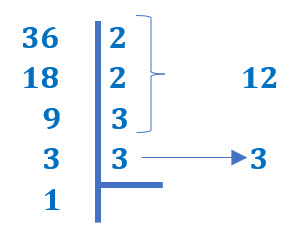
Como los signos son iguales, se buscan dos números cuya suma sea igual al coeficiente del segundo término del trinomio y cuyo producto sea igual al tercer término del trinomio, en este caso son el 12 y el 3