Profundiza el contenido con este video:
Te recomiendo estudiar estos temas antes de comenzar esta lección:
Zona de descargas:
Una inecuación cuadrática es una expresión de desigualdad que se soluciona como ecuación cuadrática.
Concepto
La expresión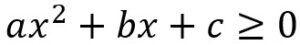 
se llama inecuación cuadrática. En ésta los límites del conjunto solución estarán determinados por las soluciones de la ecuación cuadrática 
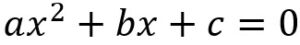, en la cual se pueden aplicar cualesquiera de los métodos conocidos.
Algunas recomendaciones para resolver desigualdades cuadráticas:
Las desigualdades cuadráticas son desigualdades en donde la variable tiene como mayor exponente el número dos; y para resolverlas, podemos seguir las siguientes recomendaciones:
Se trasladan todos los términos, al miembro de la izquierda, y se deja cero en el miembro de la derecha. Esto significa que la desigualdad se debe escribir en su forma canónica:
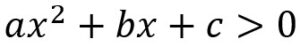o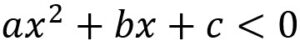 
(≤ o ≥)Se debe factorizar el miembro izquierdo. Si resulta difícil factorizar se puede aplicar la fórmula general de la ecuación cuadrática o el método de completando el cuadrado. En caso de que no se pueda resolver, entonces la solución es trivial: R o ∅.
Halle los números o valores críticos, estos números se encuentran igualando a cero, cada factor. Luego coloque esos valores en la recta real.
Confeccionar una tabla
Escriba en la tabla los intervalos que se obtienen al ubicar los números críticos en la recta real.
Tomar valores de pruebas, y evaluar los factores con los valores de pruebas.
Luego escribir la solución, considerando sólo los intervalos donde se satisface la desigualdad, tomando en cuenta el signo de la desigualdad.
Ejemplo 1:
Resuelva la siguiente inecuación cuadráticas. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
Solución:
Factorizando obtenemos:
Igualando a cero cada factor, tenemos:
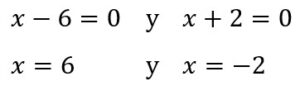
Los puntos críticos son: x=-2 y x=6
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -2
Un número mayor que -2, pero menor que 6
Un número mayor que 6
Veamos:
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad (x-6) (x+2) ≤ 0 se cumple cuando -2 < x < 6. A este intervalo hay que unirle el valor 6 y -2, pues en él la desigualdad es igual a cero. La solución es por tanto -2 ≤ x ≤ 6
Notación de intervalo: [-2, 6]
Notación de conjunto: S={x ∈ R/ -2 ≤ x ≤ 6}
Ejemplo 2:
Resuelva la siguiente inecuación cuadráticas. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
Solución:
Factorizando obtenemos:
Igualando a cero cada factor, tenemos:
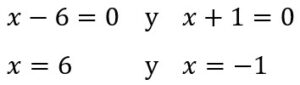
Los puntos críticos son: x=-1 y x=6
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -1
Un número mayor que -1, pero menor que 6
Un número mayor que 6
Veamos:
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad (x-6) (x+1) > 0 se cumple cuando x < -1 o x > 6. La solución es por tanto x < -1 o x > 6
Notación de intervalo: (-∞, -1) U (6, +∞)
Notación de conjunto: S={x ∈ R/ x < -1 o x >6}
Ejemplo 3:
Resuelva la siguiente inecuación cuadráticas. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
Solución:
Simplificamos
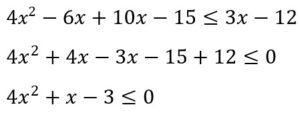
Factorizando obtenemos:
Igualando a cero cada factor, tenemos:
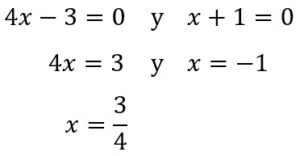
Los puntos críticos son: x=-1 y x=3/4
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -1
Un número mayor que -1, pero menor que 3/4
Un número mayor que 3/4
Veamos:
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad (4x – 3) (x+1) ≤ 0 se cumple cuando -1 < x < 3/4. A este intervalo hay que unirle el valor -1 y 3/4 , pues en él la desigualdad es igual a cero. La solución es por tanto -1 ≤ x ≤ 3/4
Notación de intervalo: [-1, 3/4]
Notación de conjunto: S={x ∈ R/ -1 ≤ x ≤ 3/4}
Gráfica:
Aprende más sobre este tema aquí:
- ¿Cómo graficar una desigualdad?
