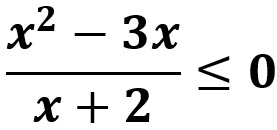Profundiza el contenido con este video:
Te recomiendo estudiar estos temas antes de comenzar esta lección:
Zona de descargas:
Las inecuaciones racionales son desigualdades que involucran expresiones racionales. Una expresión racional es aquella en la que aparecen fracciones, es decir, cocientes de polinomios. Por lo tanto, una inecuación racional implica que al menos una de las expresiones en la desigualdad es una función racional.
Por ejemplo, una inecuación racional podría tener la forma:
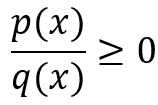
donde p(x) y q(x) son polinomios y q(x)≠0 para evitar divisiones por cero. También pueden existir inecuaciones racionales con otras relaciones de desigualdad, como <, >, ≤ o ≥
Ejemplos de estas inecuaciones son:
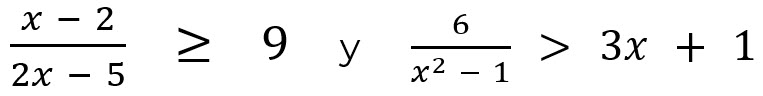
Las desigualdades racionales son representadas por una fracción algebraica y no se pueden resolver como una ecuación, es decir, que no se pueden multiplicar por el denominador para simplificar la fracción ya que este puede ser positivo o negativo.
Resolución de inecuaciones racionales
Las desigualdades racionales se resuelven de manera similar a una desigualdad cuadrática, utilizando el numerador y el denominador como factores de la fracción.
Algunas recomendaciones para resolver desigualdades racionales:
Se trasladan todos los términos, al miembro de la izquierda, y se deja cero en el miembro de la derecha. Es decir, se debe pasar todos los términos al lado izquierdo y poner cero en el lado de la derecha.
Se resuelve la suma o resta de las expresiones algebraicas.
Se busca los números críticos, estos números se encuentran igualando a cero los factores del numerador y el denominador. Luego colóquelos en la recta real, y escriba los intervalos que se obtienen al ubicarlos.
Luego se resuelve similar a la desigualdad cuadrática:
Se toman valores de pruebas, y evalúan los factores con los valores de pruebas.
Se confecciona una tabla.
Luego la respuesta se obtiene seleccionando el intervalo o la unión de intervalos que satisfacen la desigualdad, considerando el signo que se obtiene en la última columna de la tabla. Si la desigualdad es mayor que cero el signo que se debe seleccionar es “+”, si es menor que cero, es el signo «-«.
Se debe recordar que debemos excluir de la solución los valores de la variable que hacen cero al denominador, ya que la división entre cero no existe.
Ejemplo 1:
Resuelva la siguiente inecuación racional. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
Solución:
Factorizando el numerador obtenemos:
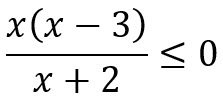
Igualando a cero cada factor, tenemos:
Los puntos críticos son: x=-2, x=0 y x=3
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -2
Un número mayor que -2, pero menor que 0
Un número mayor que 0, pero menor que 3
Un número mayor que 3
Veamos:
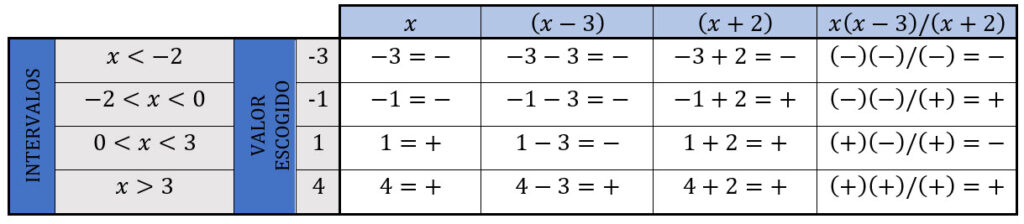
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad 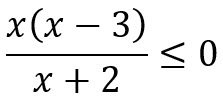se cumple cuando x < -2 y 0 < x < 3. A estos intervalos hay que unirle además los valores 0 y 3, pues en ellos la fracción se anula, no así el valor -2, ya que el denominador no puede dar resultado 0. La solución es por tanto la unión de intervalos (-∞, -2) U [0, 3].
Notación de intervalo: (-∞, -2) U [0, 3].
Notación de conjunto: S={x ∈ R/ x < -2 o 0 ≤ x ≤ 3}
Ejemplo 2:
Resuelva la siguiente inecuación racional. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
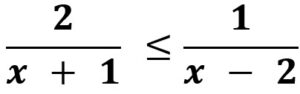
Solución:
Igualando a cero cada factor, tenemos:
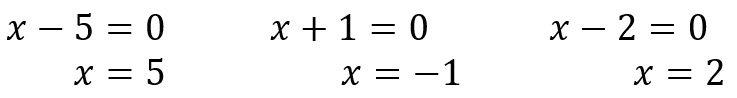
Los puntos críticos son: x=-1, x=2 y x=5
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -1
Un número mayor que -1, pero menor que 2
Un número mayor que 2, pero menor que 5
Un número mayor que 5
Veamos:
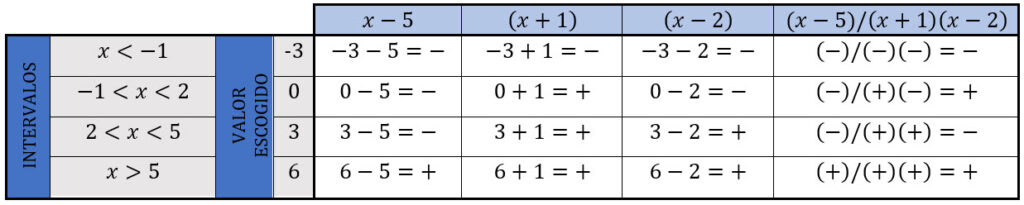
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad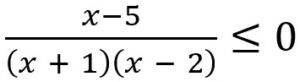 
, se cumple cuando x < -1 y 2 < x < 5. A estos intervalos hay que unirle además el 5, pues en ellos la fracción se anula, no así el valor -1 y 2, ya que el denominador no puede dar resultado 0. La solución es por tanto la unión de intervalos (-∞, -1) U (2, 5].
Notación de intervalo: (-∞, -1) U (2, 5]
Notación de conjunto: S={x ∈ R/ x < -1 o 2 < x ≤ 5}
Ejemplo 3:
Resuelva la siguiente inecuación racional. Expresar los resultados en notación de conjunto, en notación de intervalo y hacer la gráfica.
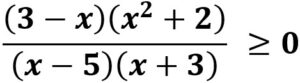
Solución:
Igualando a cero cada factor, tenemos:
Los puntos críticos son: x=-3, x=3 y x=5
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor que -3
Un número mayor que -3, pero menor que 3
Un número mayor que 3, pero menor que 5
Un número mayor que 5
Veamos:
Nota: cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+); cuando la desigualdad es < o ≤ se escogen como respuestas los intervalos que dieron respuestas negativas (-).
La desigualdad 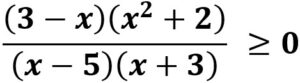, se cumple cuando x < -3 y 3 < x < 5. A estos intervalos hay que unirle además el 3, pues en él la fracción se anula, no así el valor 5 y -3, ya que el denominador no puede dar resultado 0. La solución es por tanto la unión de intervalos (-∞, -3) U [3, 5).
Notación de intervalo: (-∞, -3) U [3, 5)
Notación de conjunto: S={x ∈ R/ x < -3 o 3 ≤ x < 5}
