Profundiza el contenido con este video:
Zona de descargas:
Antes de establecer el concepto de función, veamos algunos conceptos:
Dominio: son los valores de entrada permitidos.
Codominio o Rango: indica los valores de salida correspondientes.
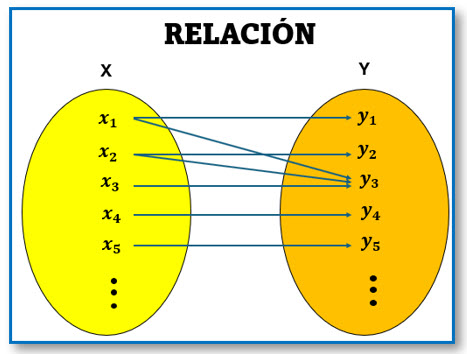
Relación: Una relación es una regla de correspondencia entre los elementos de dos conjuntos. En otras palabras, es un conjunto de pares ordenados, generalmente entre dos conjuntos.
Veamos ahora algunas definiciones de funciones:
Definición de función: |
1) Una función f es una regla que asigna a cada elemento x en un conjunto A exactamente un elemento, llamado f(x), en un conjunto B. |
2) Es una regla de correspondencia que asocia a los elementos de dos conjuntos. La cual a cada elemento del primer conjunto (dominio) le asocia un solo elemento del segundo conjunto (codominio). |
3) Una función es una colección de pares ordenados con la siguiente propiedad: Si (a, b) y (a, c) pertenecen a una colección, entonces se cumple que b=c; es decir, en una función no puede haber dos pares con el mismo primer elemento. |
4) Es una relación entre un conjunto de entradas (llamado dominio) y un conjunto de salidas (llamado codominio), donde cada entrada se relaciona con exactamente una salida. |
En resumen, la diferencia principal entre una función una relación es que en una función, cada elemento del dominio está asociado con exactamente un elemento del codominio, mientras que una relación, no existe tal restricción.
Veamos los siguientes diagramas:
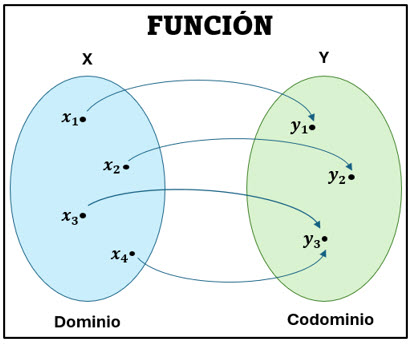
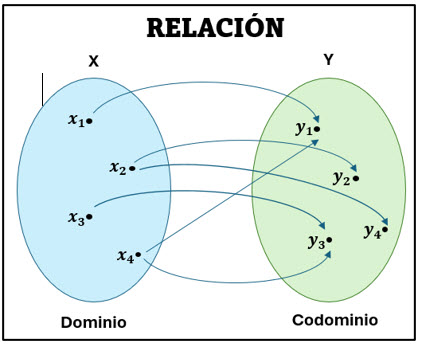
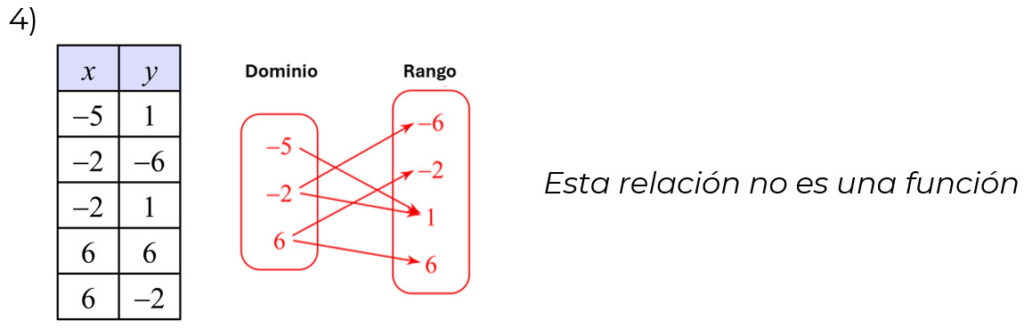
En el primer diagrama a cada elemento del dominio se le asigna un solo elemento del codominio, por lo tanto, es una función. En el segundo diagrama en el dominio vemos que al x2 le corresponden 2 elementos del codominio (y2 y4) y al x4 le corresponden 2 elementos del codominio (y1 y3), por lo tanto, es una relación.
Nota: Todas las funciones también son relaciones, pero no todas las relaciones son funciones.
PRUEBA DE LA RECTA VERTICAL
Si cada recta vertical que cruza a la gráfica de una ecuación a lo mucho en un punto, entonces la gráfica es la gráfica de una función. Por otra parte, si alguna recta vertical cruza a una gráfica de una ecuación más de una vez, la gráfica no es la de una función, es la gráfica de una relación.
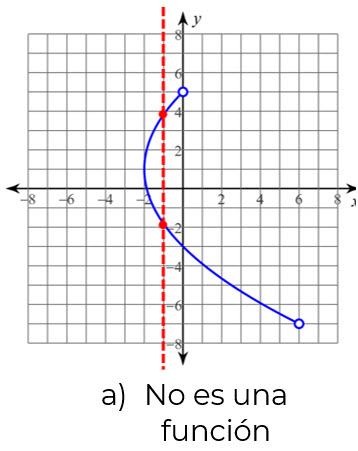
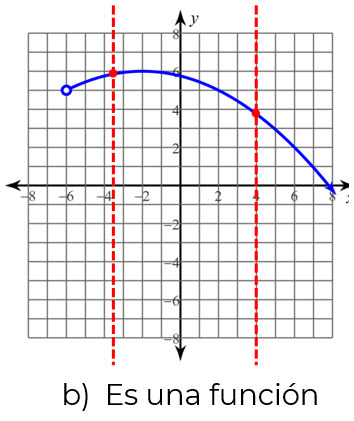
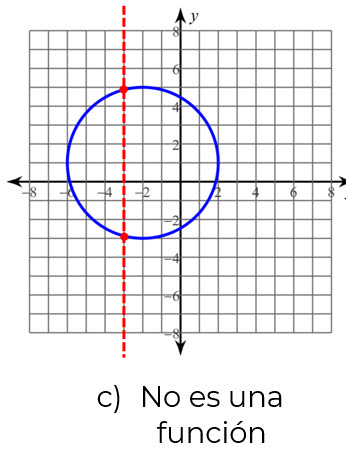
Nota: Si en alguna parte de la gráfica choca la recta vertical en más de un punto, no es una función.
VEAMOS ALGUNOS EJERCICIOS
Cada conjunto de pares ordenados representa una relación. Determine el dominio/rango y si la relación es una función:



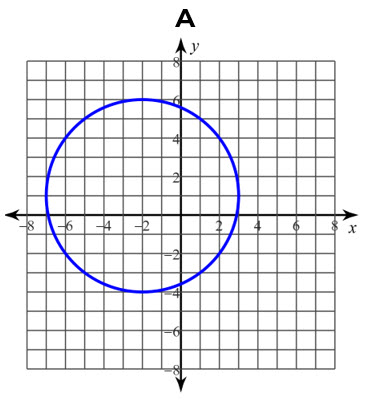
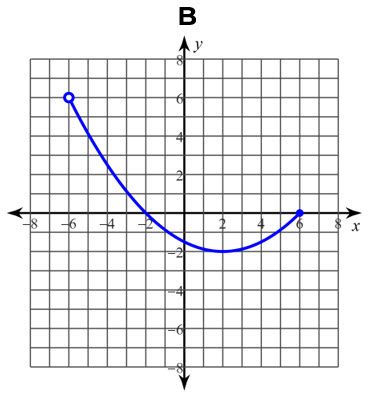
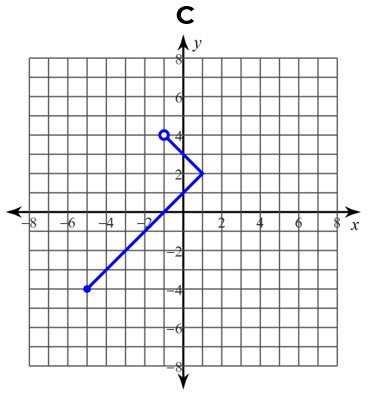
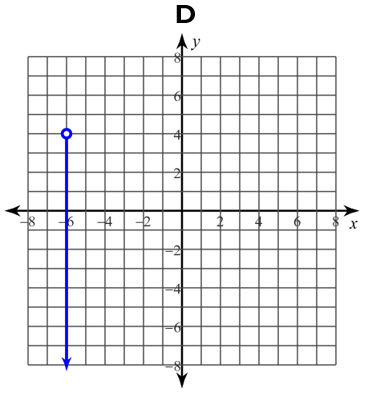
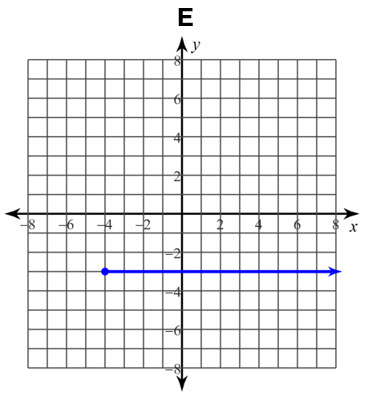
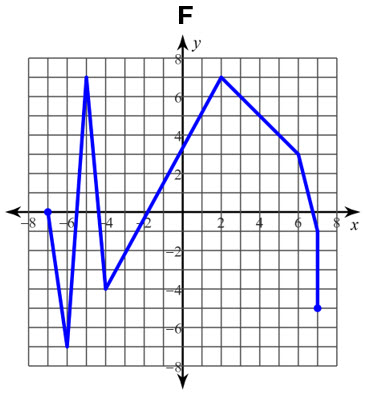
Cada gráfica representa una relación. Determine si es una función con la prueba de la recta vertical:
A, no es una función
B, si es una función
C, no es una función
D, no es una función
E, si es una función
F, no es una función (Observe cuando x=7)
CLASIFICACIÓN DE LAS FUNCIONES
Una función se denota como y=f(x), en donde:
x: variable independiente.
y: variable dependiente.
f: función, regla de asignación o correspondencia.
Las funciones se clasifican en: algebraicas y trascendentes.
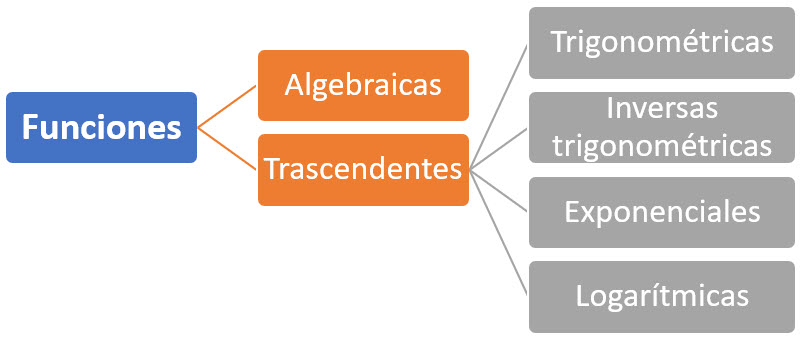
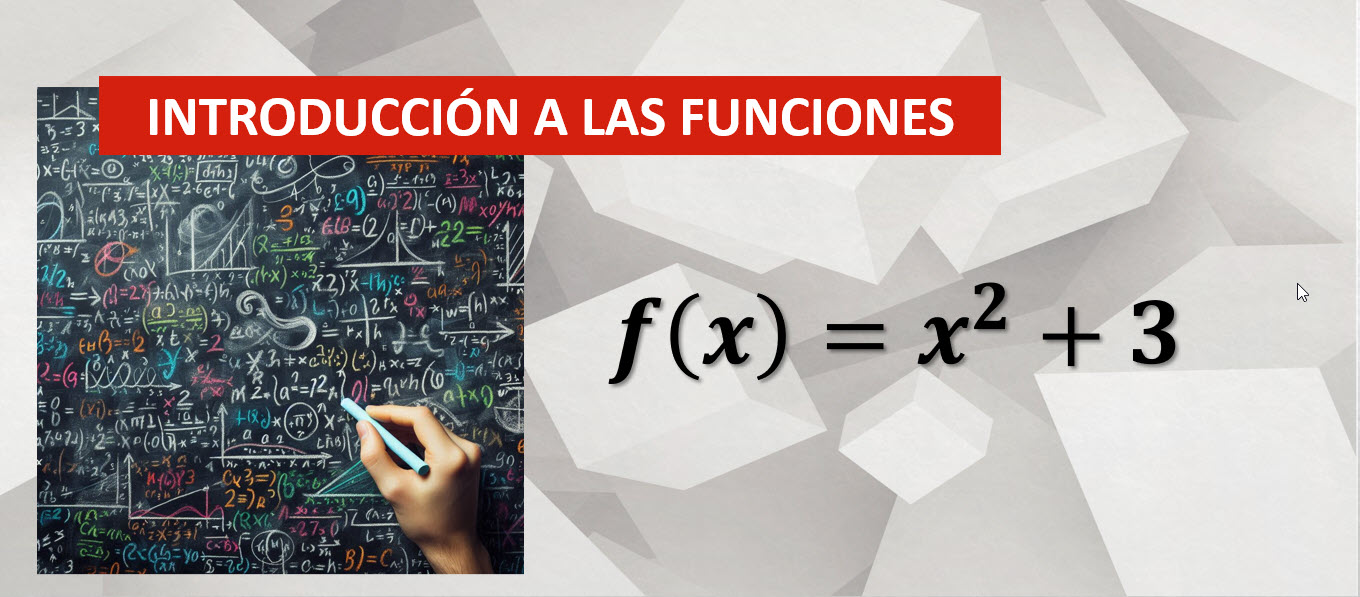
Ejemplo de funciones algebraicas:
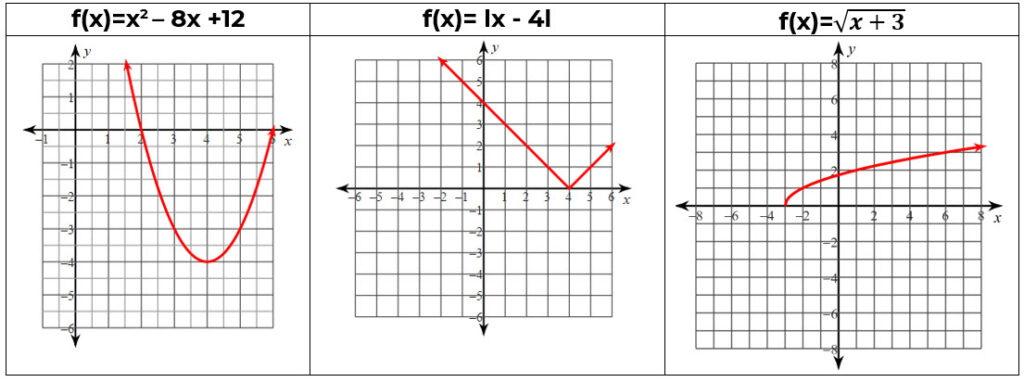
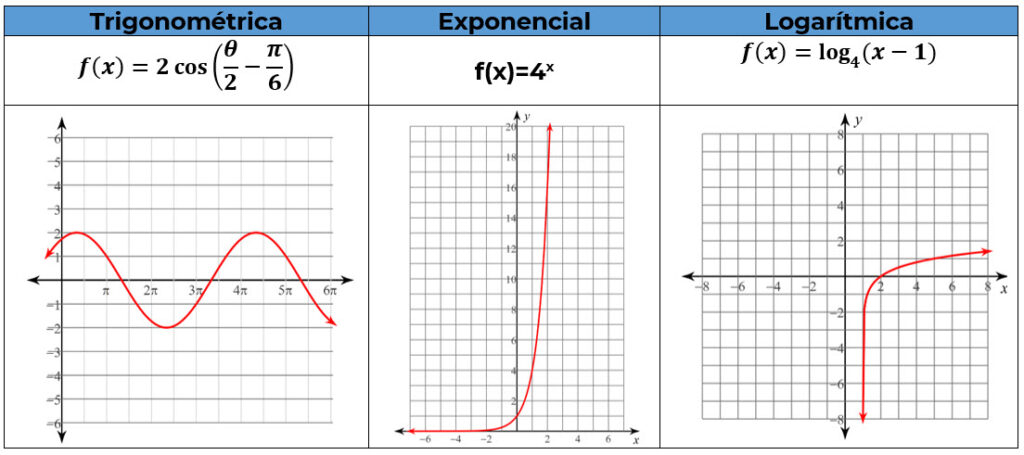
Ejemplo de funciones trascendentes: