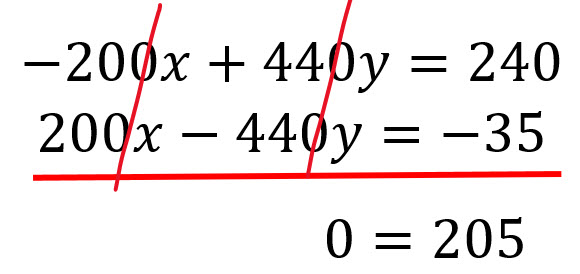Te recomiendo estudiar estos temas antes de comenzar esta lección:
- Ecuaciones lineales
Zona de descargas:
Un sistema lineal de dos ecuaciones con dos variables es un sistema escrito de la siguiente manera:
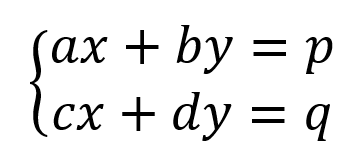
Los sistemas de ecuaciones lineales son herramientas matemáticas que se utilizan para representar y resolver situaciones en las que hay varias ecuaciones lineales interrelacionadas. Estos sistemas son útiles en diversas áreas, como la ingeniería, la física, la economía y la informática.
Método de reducción paso a paso:
Los pasos para resolver un problema por el método de reducción son los siguientes:
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
Se suman o restan las ecuaciones para eliminar esa variable.
Se resuelve la ecuación resultante y se encuentra el valor de la primera variable.
Se sustituye ese valor en cualquiera de las ecuaciones originales y se encuentra el valor de la segunda variable.
Método de reducción ejemplos
Profundiza el contenido con este video:
Ejemplo 1
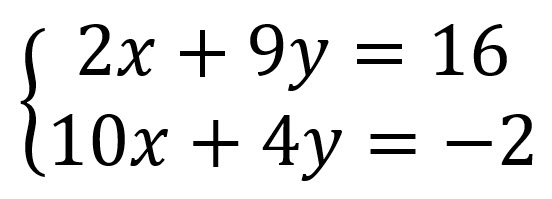
Solución:
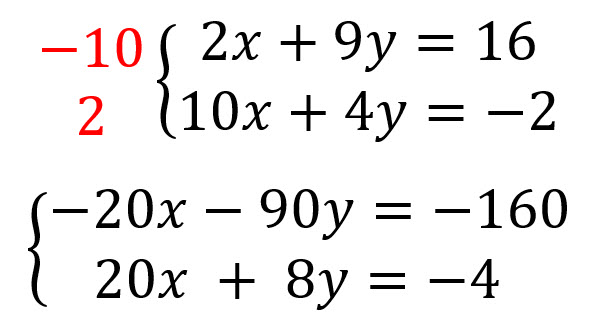
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
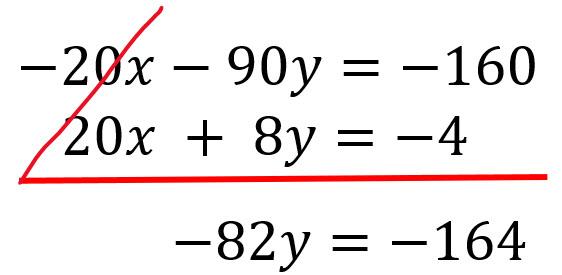
Se suman o restan las ecuaciones para eliminar esa variable.
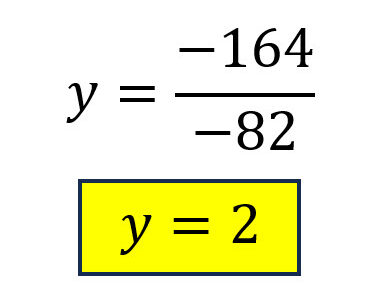
Se resuelve la ecuación resultante y se encuentra el valor de la primera variable.
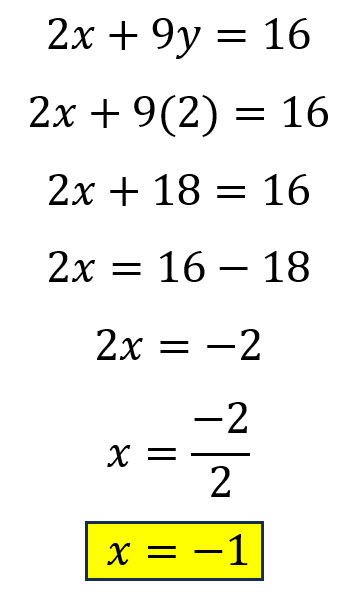
Se sustituye ese valor en cualquiera de las ecuaciones originales y se encuentra el valor de la segunda variable.
Ejemplo 2
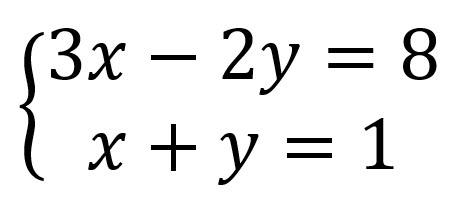
Solución:
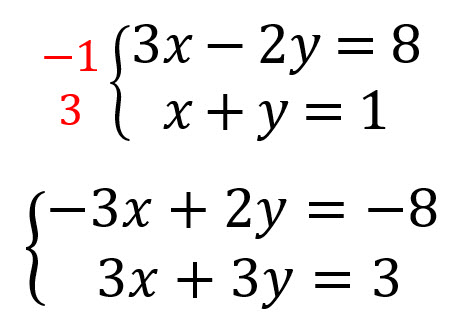
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
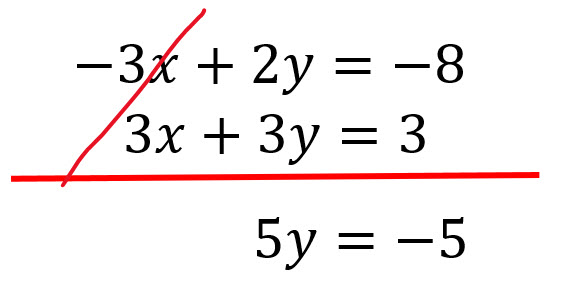
Se suman o restan las ecuaciones para eliminar esa variable.
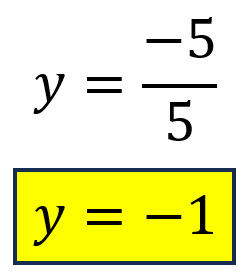
Se resuelve la ecuación resultante y se encuentra el valor de la primera variable.
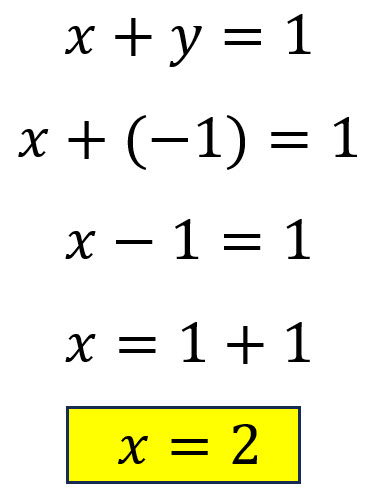
Se sustituye ese valor en cualquiera de las ecuaciones originales y se encuentra el valor de la segunda variable.
Ejemplo 3
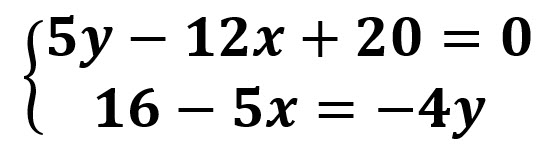
Solución:
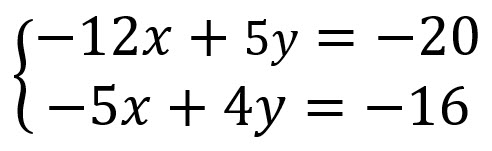
Ordenamos las ecuaciones
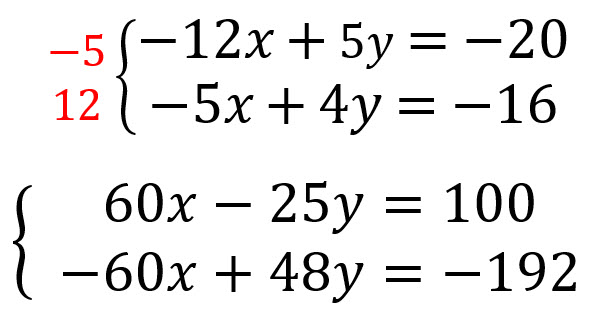
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
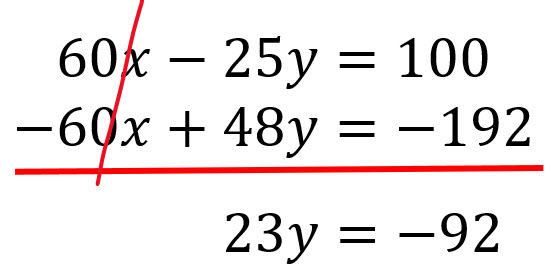
Se suman o restan las ecuaciones para eliminar esa variable.
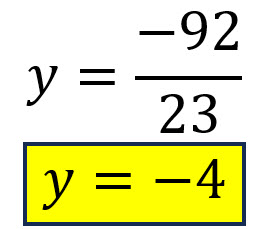
Se resuelve la ecuación resultante y se encuentra el valor de la primera variable.
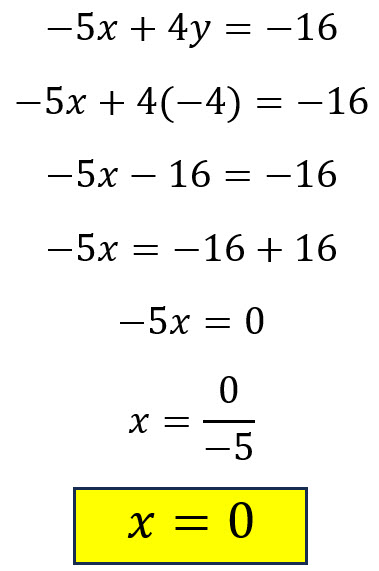
Se sustituye ese valor en cualquiera de las ecuaciones originales y se encuentra el valor de la segunda variable.
Ejemplo 4
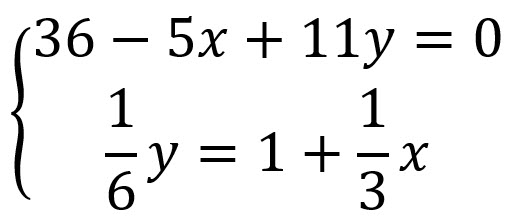
Solución:

Ordenamos las ecuaciones y quitamos los denominadores
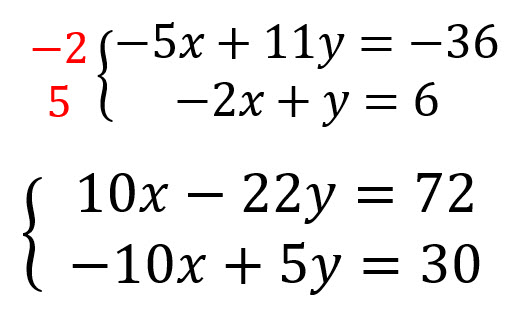
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
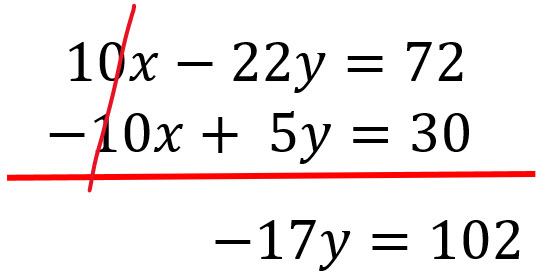
Se suman o restan las ecuaciones para eliminar esa variable.
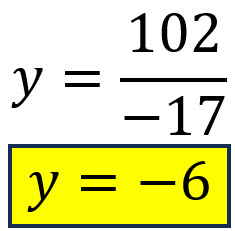
Se resuelve la ecuación resultante y se encuentra el valor de la primera variable.
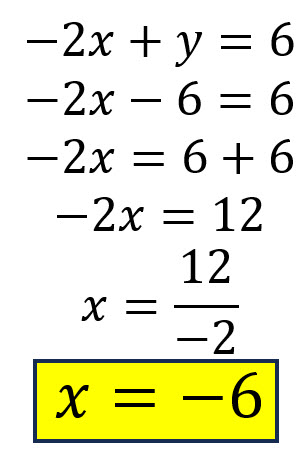
Se sustituye ese valor en cualquiera de las ecuaciones originales y se encuentra el valor de la segunda variable.
Ejemplo 5
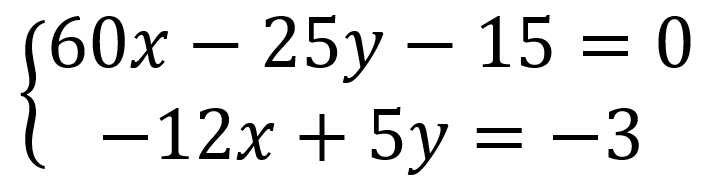
Solución:
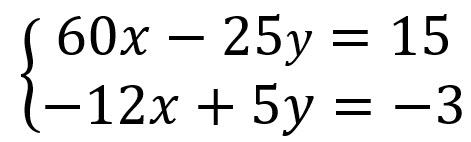
Ordenamos las ecuaciones
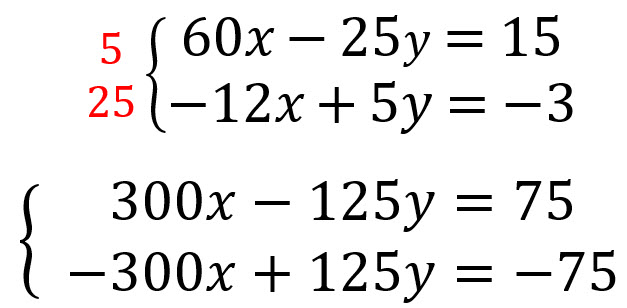
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.
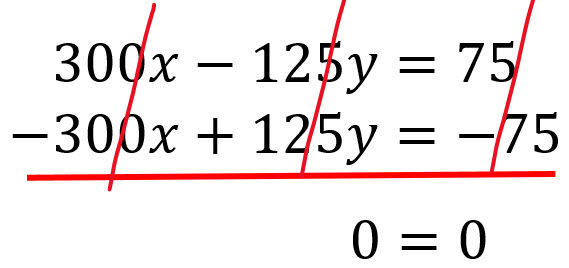
Se suman o restan las ecuaciones para eliminar esa variable.
Cuando la ecuación nos da un resultado 0=0, entonces hay infinitas soluciones.
Ejemplo 6
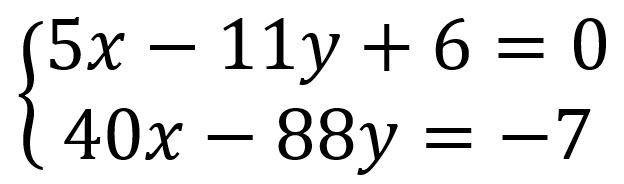
Solución:
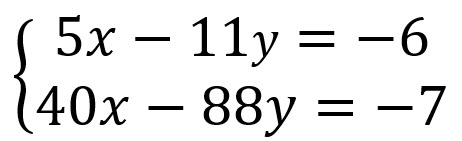
Ordenamos las ecuaciones
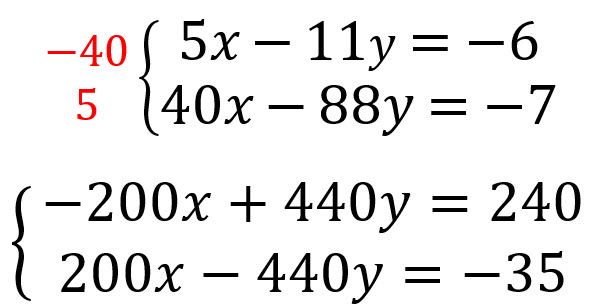
Se multiplican las ecuaciones por aquellos números que hagan que una de las variables se pueda eliminar.