Profundiza el contenido con este video:
Zona de descargas:
Son inecuaciones en las cuales, después de realizar las operaciones necesarias para quitar paréntesis y denominadores, para reducir términos semejantes, etc., el grado más alto que tiene la variable es uno; como en los siguientes casos:
ax+b>0
ax+b<0
ax+b≥0
ax+b≤0
Resolver una inecuación implica hallar los valores en los cuales se cumple la desigualdad.
Algunas recomendaciones para resolver una desigualdad lineal
Se trasladan al miembro de la izquierda los términos que contienen la variable, y al miembro de la derecha los términos constantes (términos libres o independientes).Transposición de términos.
Se efectúa la suma algebraica de los términos en cada miembro, es decir, se aplica la reducción de términos semejantes.
Si el coeficiente de la variable resulta en un número negativo, se debe multiplicar por toda la desigualdad, y se invierte el sentido de la desigualdad.
Para despejar la incógnita o variable, se divide los dos miembros de la desigualdad entre el coeficiente de la variable.
En caso de que hubiese denominadores:
Se quitan denominadores si los hubiera, de tal manera que queden coeficientes enteros. Es decir, es posible suprimir denominadores en una desigualdad sin que varíe el signo de la desigualdad, porque ello equivale a multiplicar todos los términos de la desigualad, o sea cada término de los dos miembros, por el m. c. m. de los denominadores.
Resolveremos
ahora algunas desigualdades utilizando las propiedades anteriores. Resolver una
desigualdad consiste en encontrar todas las soluciones numéricas reales.
Ejemplos:
1. Dada la siguiente inecuación x+3<-2, halle el conjunto solución y grafíquelo.
Solución:
x+3<-2
x<-2-3 (Trasladamos los términos que no contengan letras)
x<-5 (Reducimos términos semejantes)
Así, el conjunto solución que simbolizaremos con la letra S, es entonces
S=(–∞, -5) a esta solución se le denomina notación de intervalo.
S={x∈R: x<-5} a esta solución se le denomina notación de conjunto
Gráficamente:
Aprende más sobre este tema aquí:
- ¿Cómo graficar una desigualdad?
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es menor que menos cinco”.
2. Dada la siguiente inecuación 7x+3 > 8x-2, halle el conjunto solución y grafíquelo.
Solución:
7x+3 > 8x-2
7x-8x > -2-3 (Transponemos términos)
-x > -5 (Reducimos términos semejantes)
(-1)( -x > -5 ) (Multiplicando por -1 e invertimos el sentido de la
desigualdad)
x < 5
Así, el conjunto solución que simbolizaremos con la letra S, es entonces
S=(–∞, 5)
S={x∈R: x < 5}
Gráficamente
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es menor que cinco”.
3. Dada la siguiente inecuación 5x ≥ 10, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = [2, +∞)
S={x∈R: x ≥ 2}
Gráficamente:
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es mayor o igual que dos”.
4. Dada la siguiente inecuación -3x – 2 < 7, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = (-3, +∞)
S={x∈R: x > -3}
Gráficamente:
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es mayor que menos tres”.
5. Dada la siguiente inecuación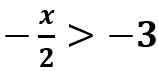 
, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = (-∞, 6)
S={x∈R: x < 6}
Gráficamente:
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es menor que seis”.
6. Dada la siguiente inecuación 2(x + 1) -1 < x + 3, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = (-∞, 2)
S={x∈R: x < 2}
Gráficamente:
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es menor que dos”.
7. Dada la siguiente inecuación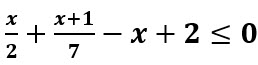 
, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = [6, +∞)
S={x∈R: x ≥ 6}
Gráficamente
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde equis es mayor o igual que seis”.
8. Dada la siguiente inecuación – 8 ≤ 3x – 5 < 7, halle el conjunto solución y grafíquelo.
Solución:
Así, el conjunto solución que simbolizaremos con la letra S, es entonces:
S = [ -1, 4)
S={x∈R: -1 ≤ x < 4}
Gráficamente:
Expuesta esta relación, se lee: “equis es elemento de los números reales en donde menos uno es menor o igual que equis, equis es menor que cuatro”.
