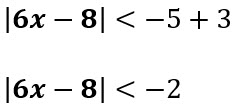Profundiza el contenido con este video:
Te recomiendo estudiar estos temas antes de comenzar esta lección:
Zona de descargas:
Concepto de Valor Absoluto
Cualquier número «x» tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto x al origen. Podemos interpretar que la distancia del 3 al origen es 3 unidades, igual que la distancia del punto -3 al origen es 3.
En notación, esto es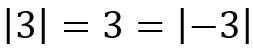 
(las barras se leen como el valor absoluto de la cantidad que está dentro de ellas).
En el valor absoluto no importa en qué lado de la recta real está representado el número. Analíticamente, podemos ver que si x es positivo, es decir, está a la derecha del cero, entonces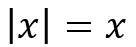 
; y si está a la izquierda del origen, es decir, si x es negativo, entonces 
.
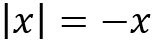Definición
Si x es un número real (x∈ℜ), el valor absoluto de x se escribe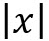 
y se define por:
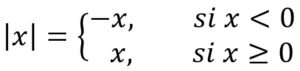
Ejemplo 1:
Resuelva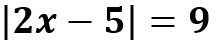 
Escriba la ecuación con valor absoluto como dos ecuaciones lineales y resuelva cada ecuación lineal:
Ejemplo 2:
Resuelva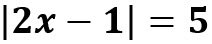 
Escriba la ecuación con valor absoluto como dos ecuaciones lineales y resuelva cada ecuación lineal:
Aprende más sobre este tema aquí:
- ¿Cómo graficar una desigualdad?
Inecuaciones con valor absoluto
Para resolver inecuaciones que involucran valor absoluto; expresiones algebraicas de la forma ax+b, donde a y b son constantes reales con a≠0, y x es una variable real, se utiliza la definición de valor absoluto y se aplican algunas de las propiedades, con el fin de facilitar el procedimiento de resolución.
Así, siendo c>0:
Ejemplo 1:
Resuelva la siguiente inecuación con valor absoluto: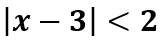 
Solución:
Utilizando (i) tenemos que:
Ejemplo 2:
Resuelva la siguiente inecuación con valor absoluto: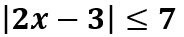 
Solución:
Utilizando (ii) tenemos que:
Ejemplo 3:
Resuelva la siguiente inecuación con valor absoluto: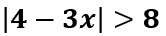 
Solución:
Utilizando (iii) tenemos que:
Ejemplo 4:
Resuelva la siguiente inecuación con valor absoluto: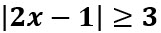 
Solución:
Utilizando (iv) tenemos que:
Ejemplo 5:
Resuelva la siguiente inecuación con valor absoluto: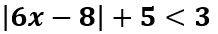 
Solución:
siempre será mayor o igual a 0 para cualquier número real x, la desigualdad nunca podrá ser verdadera. Por lo tanto, la solución es el conjunto vacío, ∅.
