Profundiza el contenido con este video:
Zona de descargas:
El dominio de una función es el conjunto de todas las entradas para la función.
En términos del plano cartesiano, el dominio corresponde al conjunto formado por los valores posibles para X.
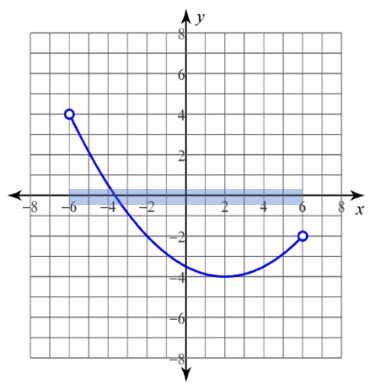
Si observamos esta gráfica, la x puede tomar valores mayores a -6 y menores que 6; por lo tanto, el dominio sería -6 < x < 6. El dominio también se puede escribir como notación de intervalo (-6, 6) y cómo notación de conjunto
El dominio de una función puede indicarse explícitamente. Por ejemplo, si escribimos:
Entonces el dominio es el conjunto de todos los números reales x para los cuales
Ahora consideremos la siguiente función: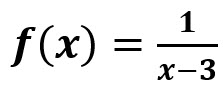 
La función f no está definida en x=3, así que su dominio son todos los números reales excepto el 3.
El dominio se puede escribir así:
DOMINIO DE UNA FUNCIÓN CONOCIENDO SU GRÁFICA
El Dominio es el conjunto de entradas o valores que puede tomar la x. En las siguientes imágenes veremos el dominio de tres funciones y otras tres funciones por partes.
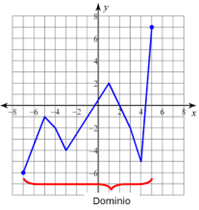
La siguiente ilustración nos muestra que el dominio serían las x mayores o iguales que -7 y menores o iguales que 5.
Se escribe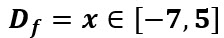 
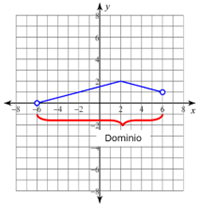
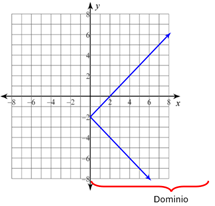
El dominio serían las x mayores que -6 y menores que 6.
Se escribe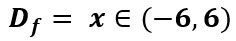 
El dominio serían las x mayores o iguales que 0, las flechas nos indican que la gráfica continúa hasta +∞
Se escribe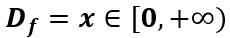 
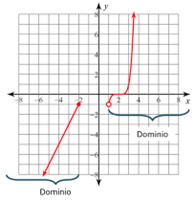
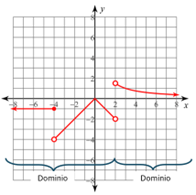
Cuando x=-4 hay una bolita rellena que le daría valor a “y”; sin embargo, cuando x=2 ambas bolitas están sin rellenar y la “y” no tiene valor. Por lo tanto, el dominio será:
Se escribe
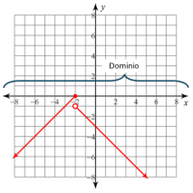
Cuando x=-2 hay una bolita rellena que le daría valor a “y”; Por lo tanto, el dominio será:
Se escribe
DOMINIO DE UNA FUNCIÓN SI NO SE CONOCE SU GRÁFICA
Importante: Si trabajamos funciones constantes, lineales, cuadráticas o cualquier tipo de función polinómica, el dominio serán todos los números reales a menos que se haya expresado el dominio de forma explícita.
El Dominio de todas estas funciones es x∈ℜ, escrito de otra manera (-∞,∞)
DOMINIO DE FUNCIONES RACIONALES
Las funciones racionales son aquellas que están definidas como el cociente de polinomios en los cuales el denominador tiene una grado mayor o igual a 1.
¿Cómo encontrar el dominio de funciones racionales?
Veamos los siguientes ejemplos:
EJEMPLO 1
Sea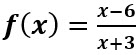 
Encuentre su dominio.
SOLUCIÓN:
El denominador debe ser distinto de cero, por lo tanto:
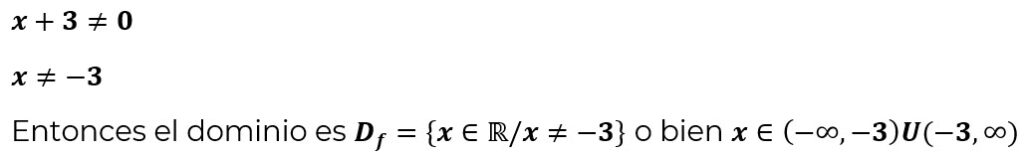
EJEMPLO 2
Sea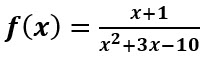 
Encuentre su dominio.
SOLUCIÓN:
El denominador debe ser distinto de cero, por lo tanto:
DOMINIO DE FUNCIONES CON RADICAL
¿Cómo encontrar el dominio de funciones con radical?
Veamos los siguientes ejemplos:
EJEMPLO 1
Sea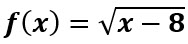 
Encuentre su dominio.
SOLUCIÓN:
Si el índice de la raíz es par, el radicando debe ser mayor o igual a cero, por lo tanto:
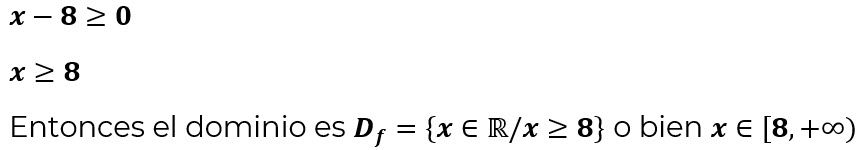
EJEMPLO 2
Sea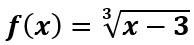 
Encuentre su dominio.
SOLUCIÓN:
Si el índice de la raíz es impar el radicando puede tomar cualquier valor.
Entonces el dominio es 
EJEMPLO 3
Sea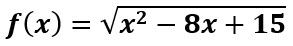 
Encuentre su dominio.
SOLUCIÓN:
El radicando debe ser mayor o igual a cero porque el índice es par, por lo tanto:
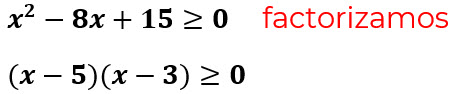
Igualamos a cero cada factor, para obtener los puntos críticos:
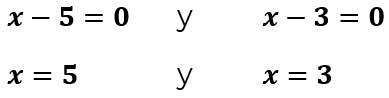
Los puntos críticos son x=5 y x=3
Para determinar el conjunto solución evaluemos la inecuación cuadrática con:
Un número menor a 3
Un número mayor a 3, pero menor que 5
Un número mayor que 5
Veamos:
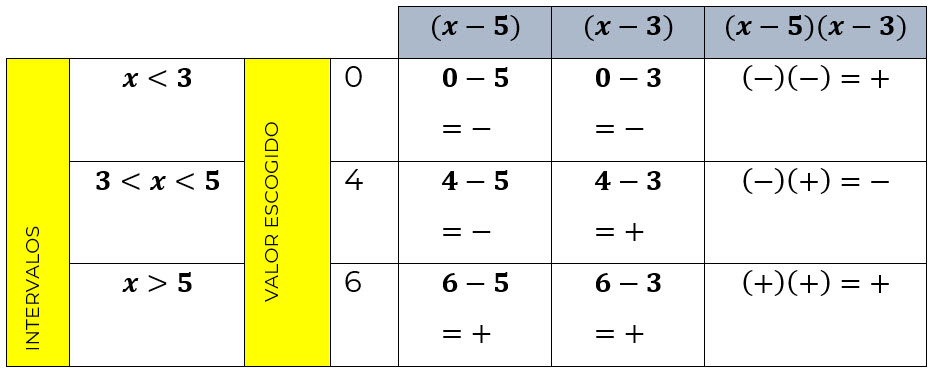
Cuando la desigualdad es ≥ se escogen como respuestas los intervalos que dieron respuestas positivas.
La desigualdad , se cumple cuando x<3 o cuando x>5. A este intervalo hay que unirle el valor 3 y 5 , pues en él la desigualdad es igual a cero. Por lo tanto la solución es x≤3 o x≥5.
El Dominio es por lo tanto
DOMINIO DE FUNCIONES LOGARÍTMICAS
¿Cómo encontrar el dominio de funciones logarítmicas?
Para determinar el dominio de funciones con logaritmos, se debe tomar en cuenta que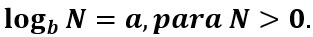 
En los logaritmos a N se le llama argumento.
Veamos los siguientes ejemplos:
EJEMPLO 1
Sea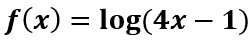 
Encuentre su dominio.
SOLUCIÓN:
El argumento debe ser mayor que cero, por lo tanto:
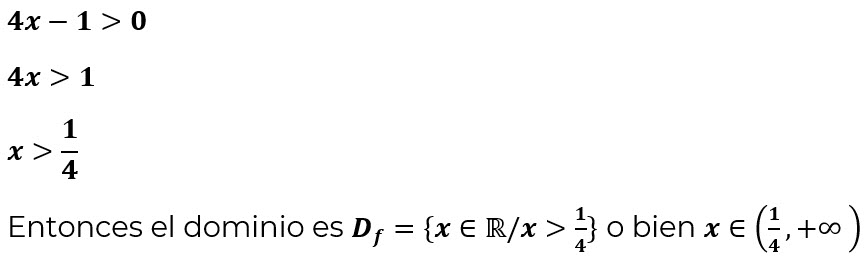
DOMINIO DE FUNCIONES COMBINADAS Y CASOS MÁS DIFÍCILES
Veamos los siguientes ejemplos:
EJEMPLO 1
Sea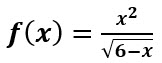 
Encuentre su dominio.
SOLUCIÓN:
EJEMPLO 2
Sea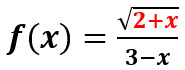 
Encuentre su dominio.
SOLUCIÓN:
EJEMPLO 3
Sea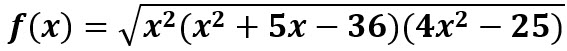 
Encuentre su dominio.
SOLUCIÓN:
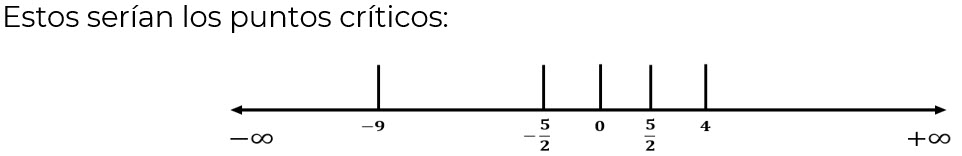
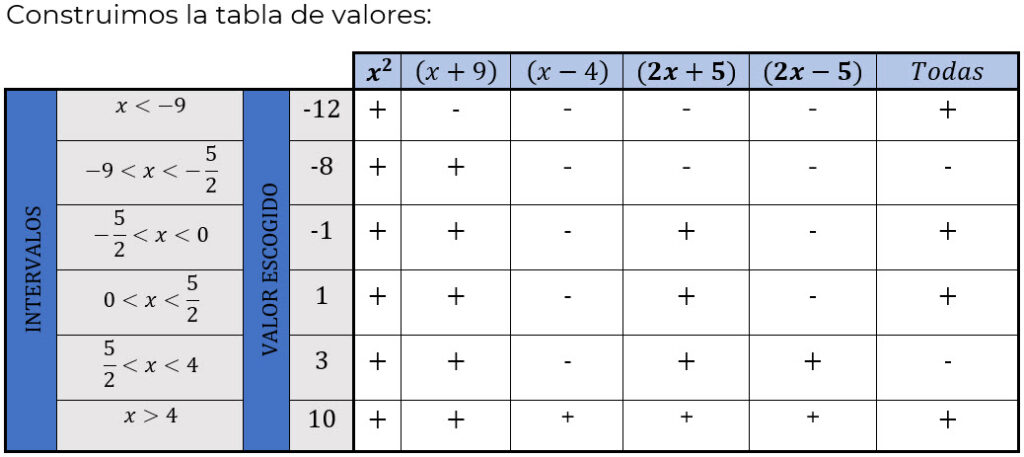
Cuando la desigualdad es > o ≥ se escogen como respuestas los intervalos que dieron respuestas positivas (+)
La desigualdad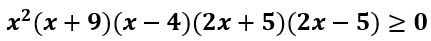 
se cumple cuando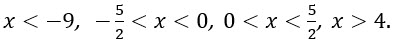 
A este intervalo hay que unirle el valor -9, -5/2, 0, 5/2 y 4, pues en él la desigualdad es igual a cero.
Entonces el dominio es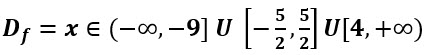 
EJEMPLO 4
Sea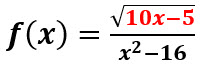 
Encuentre su dominio.
SOLUCIÓN:
En este problema tenemos que ocuparnos de la raíz cuadrada y de la división por cero. Ocupémonos primeramente de la raíz:
Ahora nos ocupamos del denominador:
Se tienen que cumplir estas dos condiciones, para que se entienda mejor haré una gráfica de la solución:
