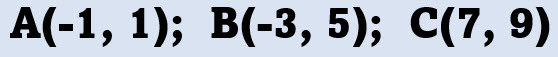Profundiza el contenido con este video:
Zona de descargas:
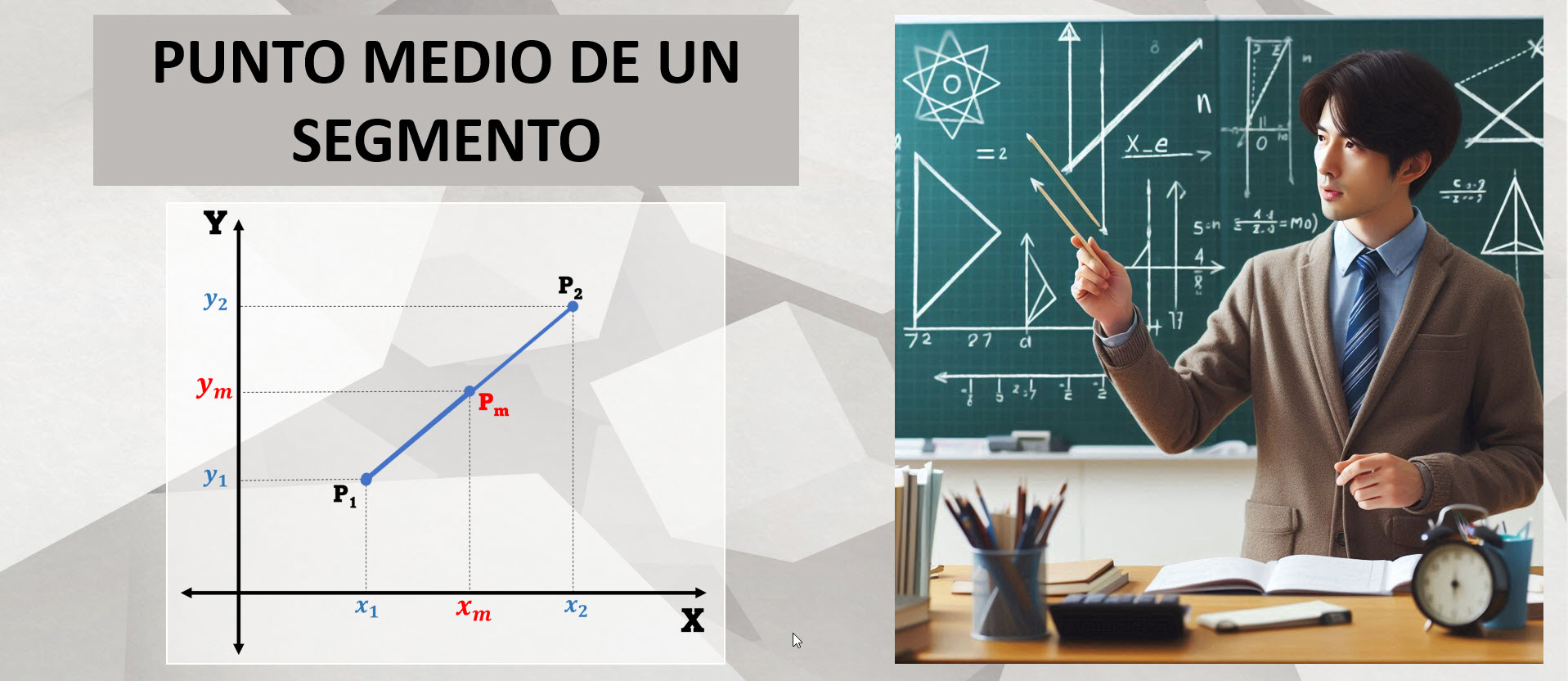
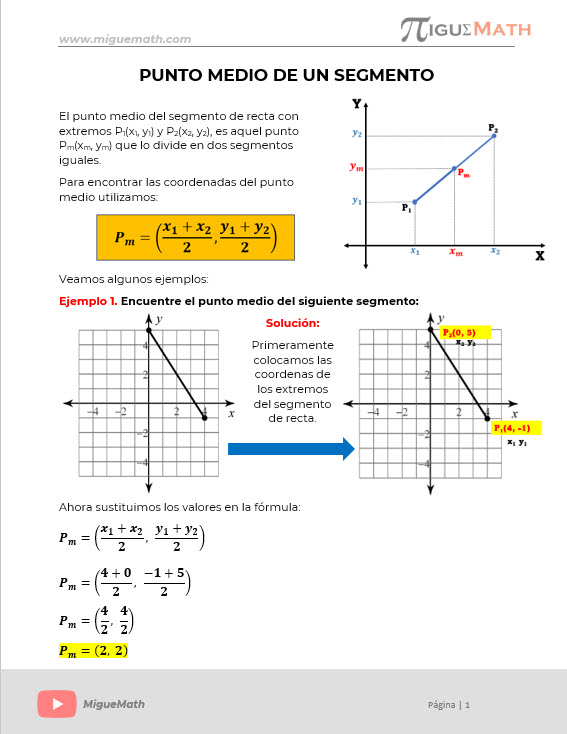
El punto medio del segmento de recta con extremos P1(x1, y1) y P2(x2, y2), es aquel punto Pm(xm, ym) que lo divide en dos segmentos iguales.
Para encontrar las coordenadas del punto medio utilizamos:
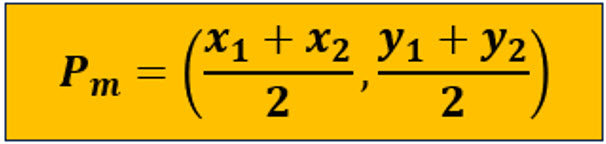
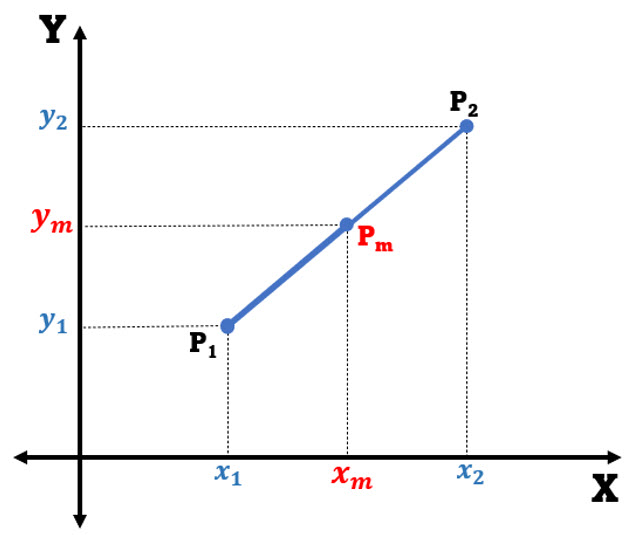
Veamos algunos ejemplos:
EJEMPLO 1
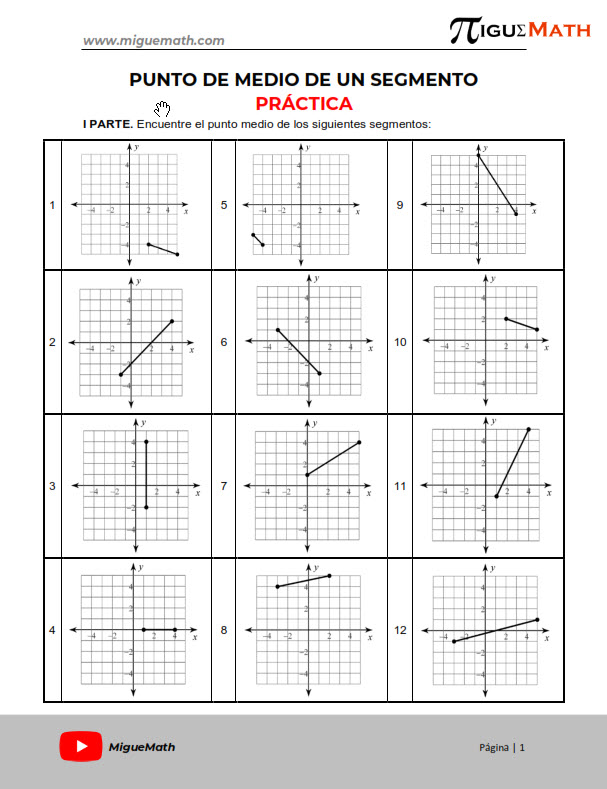
Encuentre el punto medio del siguiente segmento:
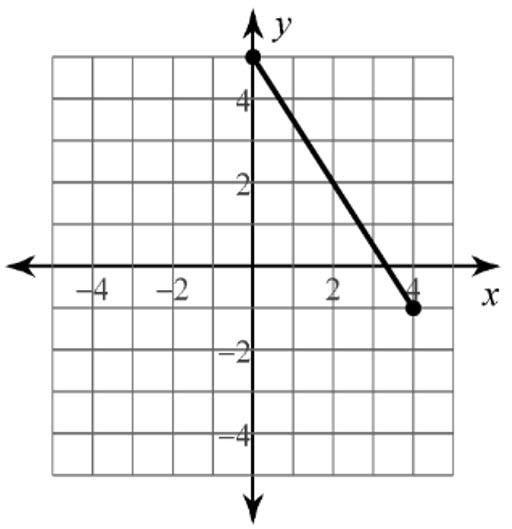
Solución:
Primeramente colocamos las coordenadas de los extremos del segmento de recta.
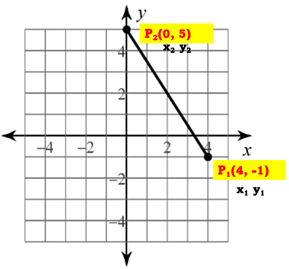
Ahora sustituimos los valores en la fórmula:
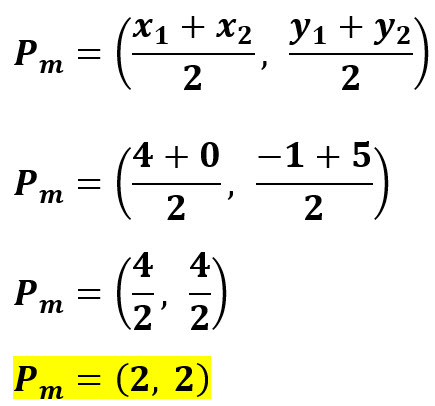
EJEMPLO 2
Encuentre las coordenadas del punto medio del segmento que une los puntos G(3,1) y F(9,1)
Solución:
Sustituimos los valores de las coordenadas de G y F en la fórmula
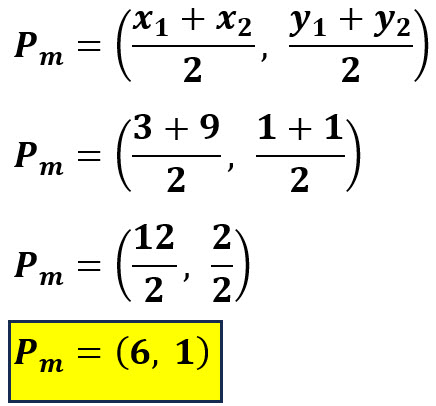
EJEMPLO 3
Uno de los extremos de un segmento de recta es el punto (4, 3) y su punto medio es el punto (-1, -3). Encuentre las coordenadas del otro extremo.
Solución:
Separamos la fórmula:
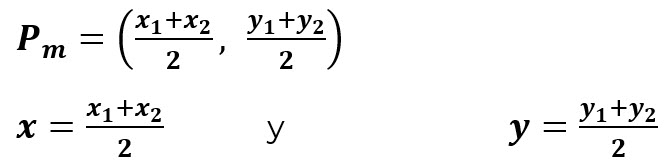
Sustituimos los valores; en este caso el punto medio nos da los valores de (x, y):
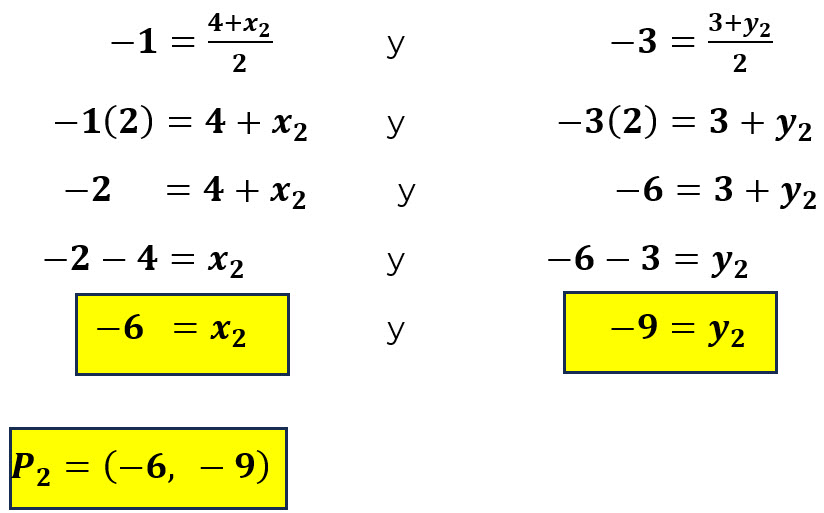
EJEMPLO 4
Los puntos medios de los lados de un triángulo son (-2, 3), (2, 7), (3, 5). Encuentra las coordenadas de los vértices.
Solución:
Hacemos el diagrama de un triángulo para visualizar mejor el problema (El Diagrama no está colocado en el plano cartesiano).
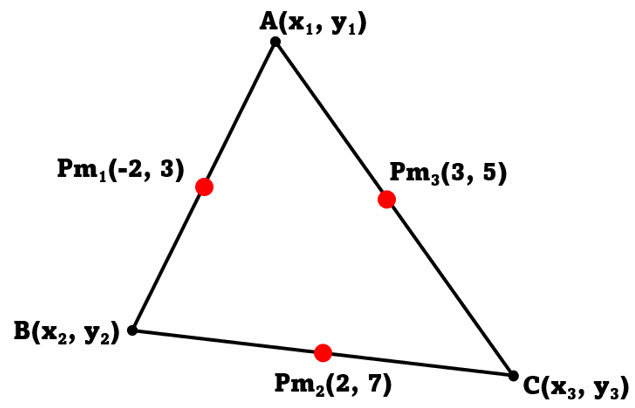
Para cada punto medio encontramos las ecuaciones resultantes.

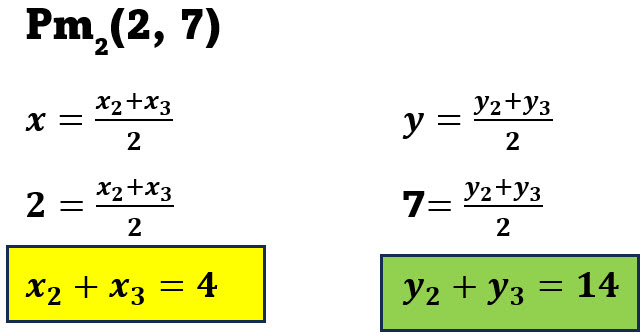

Formamos un sistema de ecuaciones con las ecuaciones que contengan x enmarcadas en amarillo.
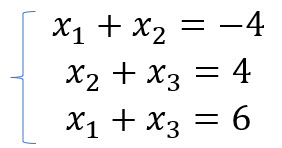
Al resolver el sistema de ecuaciones obtenemos:
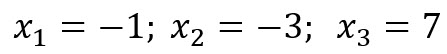
Formamos un sistema de ecuaciones con las ecuaciones que contengan y enmarcadas en verde.
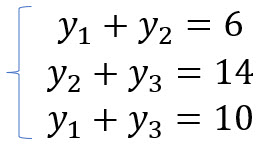
Al resolver el sistema de ecuaciones obtenemos:
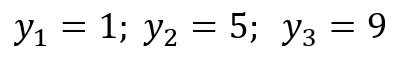
Con ambos sistemas de ecuaciones resueltos podemos deducir los valores de A, B, C: