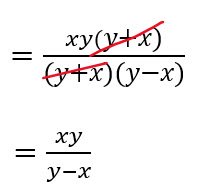Profundiza el contenido con este video:
Zona de descargas:
La potenciación es una expresión matemática que incluye dos términos denominados: base «a» y exponente «n».
Se escribe an, y se lee: «a elevado a n».
Cuando el exponente es un número natural, equivale a multiplicar la base por sí misma varias veces: el exponente indica cuántos factores iguales se multiplican.
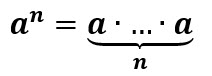
Ley de los signos:
Si la base es positiva, la potencia es positiva sea cual sea el exponente.
Ejemplo: ( 3)3=3x3x3 =27
Si la base es negativa y el exponente par, la potencia es positiva.
Ejemplo: (-3)2= (-3)(-3)=9
Si la base es negativa y el exponente impar, la potencia es negativa
Ejemplo: (-3)3=(-3)(-3)(-3)= -27
LEYES DE LOS EXPONENTES
Si y son bases cualesquiera distintas de cero y m y n enteros positivos, se tiene las siguientes leyes de los exponentes:
Multiplicación de potencias de igual base.
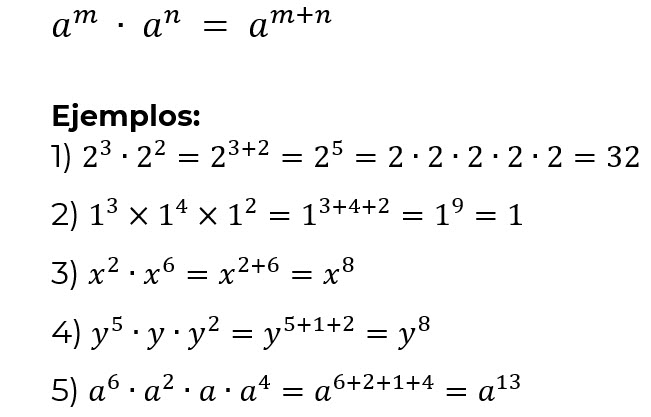
División de potencias de igual base.
Potencia de una potencia.
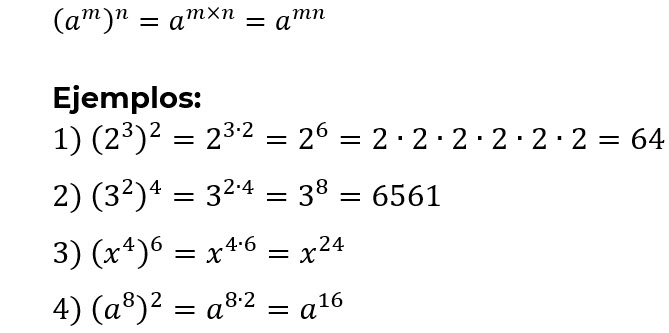
4. Potencia de un producto.
5. Potencia de un cociente.
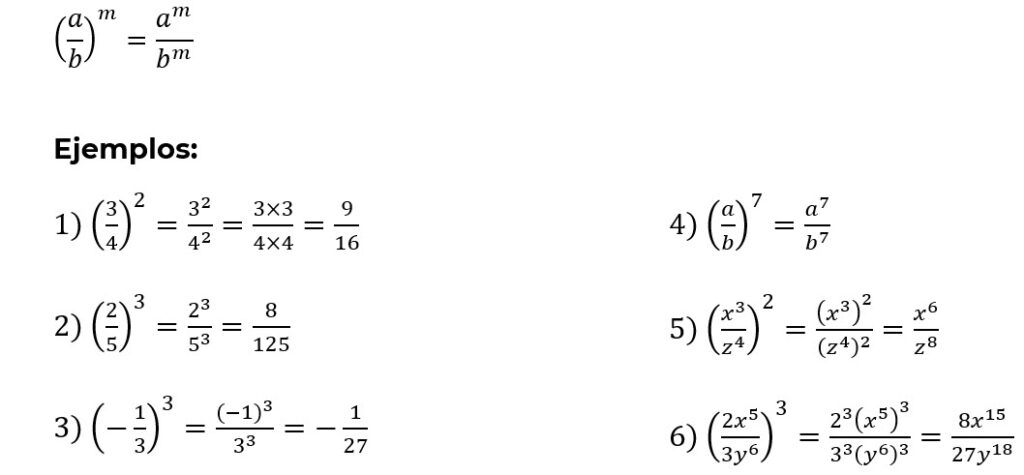
6. Exponente 0
De acuerdo con la definición de potencia, la potencia a0 carece de significado pues no existe producto cuando no hay ningún factor. Para este caso se puede dar una definición particular, pero que éste de acuerdo con las leyes de la potenciación.
Así se sabe que a5÷a5=a0, y por división de potencias de igual base, cuando los exponentes eran iguales vale la unidad.
Luego, tomaremos como definición a0=1, si a no es cero.
Todo número elevado al exponente cero es igual a la unidad.
7. Exponente 1
Toda potencia de exponente 1 es igual a la base:
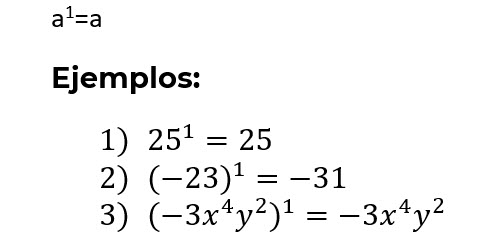
8. Exponente entero negativo
El exponente negativo resulta de dividir dos potencias de la misma base cuando el exponente de dividendo es menor que el exponte del divisor.
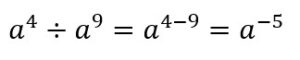
es lo mismo que:
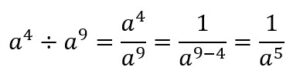
De donde observamos que:
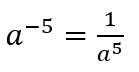
En general, toda potencia con exponente negativo es igual a la unidad dividida por la misma potencia con exponente positivo.
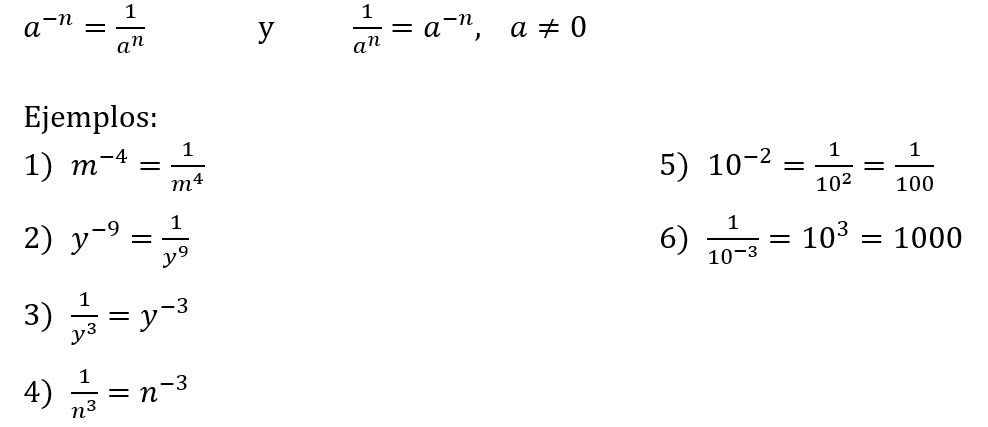
Transformación de exponentes negativos a positivos
De acuerdo con la definición del exponente negativo, veamos los siguientes ejemplos:
Cualquier factor de un término de una fracción se puede trasladar al otro término, si se cambia el signo del exponente del factor.
Cuando simplificamos una expresión significa que todas las respuestas deben expresarse usando exponentes positivos.
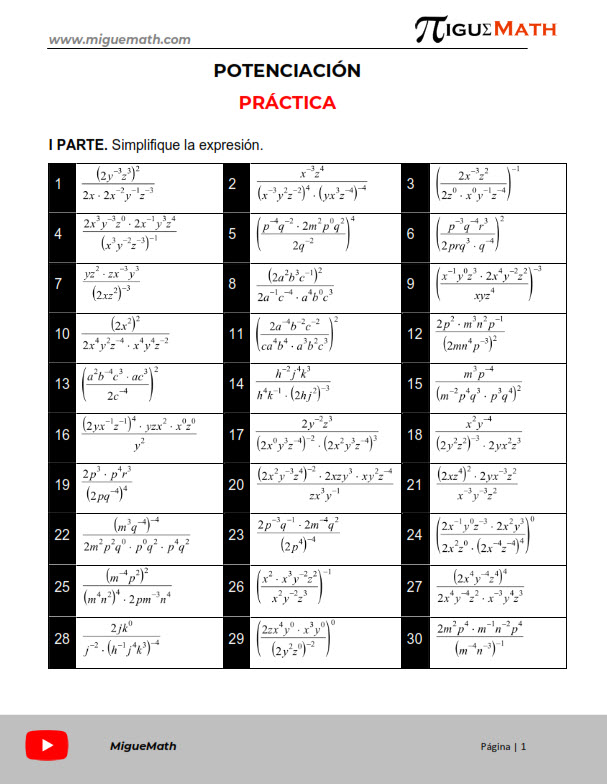
SIMPLIFICACIÓN
Los teoremas de los exponentes se aplican dependiendo de cómo esté estructurada la expresión matemática. El orden en que se usan estas reglas lo determinan las operaciones (sumas, multiplicaciones, etc.) y los paréntesis o corchetes que aparezcan en el problema.
EJEMPLO 1
Simplifica y da el resultado con exponentes positivos:
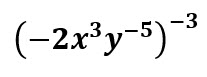
Solución:
El exponente de mayor jerarquía se convierte en positivo
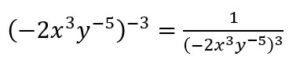
Se utiliza la propiedad potencia de un producto
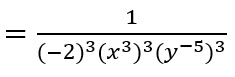
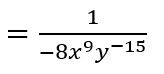
Se convierte el exponente negativo a positivo
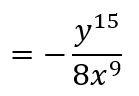
EJEMPLO 2
Simplifica y da el resultado con exponentes positivos:
Solución:
Utilizamos la propiedad potencia de una potencia:
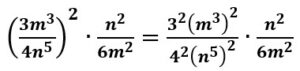
Resolvemos las potencias
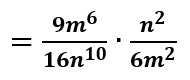
Se simplifica y se utiliza la propiedad potencia de una división
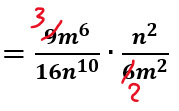
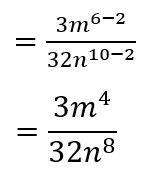
EJEMPLO 3
Simplifica y da el resultado con exponentes positivos:
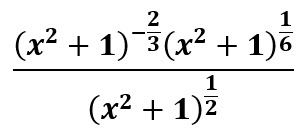
Solución:
Como la expresión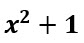 
es un binomio, trabajaremos solamente con los exponentes:
Se utiliza la propiedad multiplicación de bases igales en el numerador
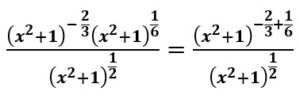
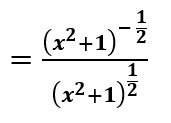
Se utiliza la propiedad división de bases iguales
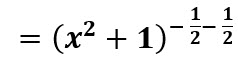
Se convierte el exponente negativo a positivo
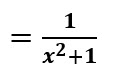
EJEMPLO 4
Simplifica y da el resultado con exponentes positivos:
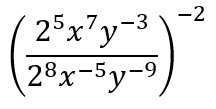
Solución:
Los exponentes negativos dentro del paréntesis los convertimos a positivos
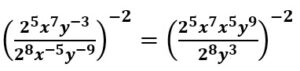
utilizamos las propiedades de multiplicación y división de bases iguales dentro del paréntesis
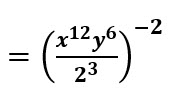
Convertimos el exponente negativo en positivo
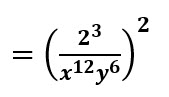
utilizamos la propiedad potencia de una potencia
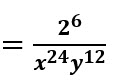
Resolvemos la potencia
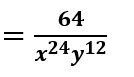
EJEMPLO 5
Convierte en una fracción equivalente en la que todos los exponentes sean positivos:
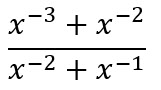
Solución:
Para eliminar los exponentes negativos, multiplicamos el numerador y el denominador por x3 (que es x elevado al valor absoluto del exponente más grande en la expresión original):
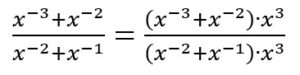
Resolvemos la multiplicación
Factorizamos el denominador
Simplificamos
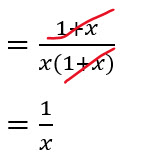
EJEMPLO 6
Convierte en una fracción equivalente en la que todos los exponentes sean positivos:
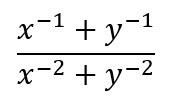
Solución:
Para eliminar los exponentes negativos, multiplicamos el numerador y el denominador por x2 ∙y2 (que es x y y elevado al valor absoluto del exponente más grande en la expresión original):
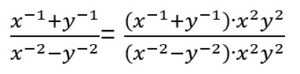
Resolvemos la multiplicación
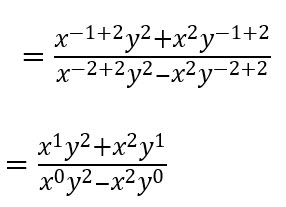
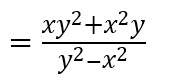
Factorizamos el numerador y el denominador
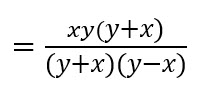
Simplificamos
