Profundiza el contenido con este video:
Zona de descargas:
Una proposición de la forma f(x) > g(x) o f(x) ≥ g(x) o f(x) < g(x) o f(x) ≤ g(x) es llamada una desigualdad.
El símbolo: “<” significa “menor que”, “>” significa “mayor que”, “≤” significa “menor o igual que” y “≥” significa “mayor o igual que”.
Algunos ejemplos de desigualdades, son los siguientes:
3 < 7,
-1 > 2,
x ≤ 2,
x – 3 ≤ 4,
- x ≥ 5
Al igual que ocurre con las igualdades, las desigualdades pueden ser ciertas o falsas. Entonces tenemos que: 3 < 7 es cierta, -1 > 2 es falsa; mientras que x ≤ 2 y x – 3 ≤ 4 dependerá del valor que le demos a x.
Una inecuación es una desigualdad en la que hay una o más incógnitas (cantidades desconocidas) y que puede cumplirse o no, es decir, que sólo se verifica para determinados valores de las incógnitas. Los valores de las incógnitas que hace que la desigualdad se cumpla se le llaman soluciones de la inecuación.
Desigualdades algebraicas
Son desigualdades que contienen números y expresiones con una o más variables.
Ejemplos:
3x + 5 < 2x
4y – 4 > 3y – 1
4 ≤x – 6 ≤ 5
Propiedades de las desigualdades
Si sumamos o restamos un mismo número a los dos miembros de una desigualdad, resulta otra del mismo sentido.
Ejemplo:
5x + 4 > 6
5x + 4 – 4 > 6 – 4
(A ambos lados restamos 4, por lo tanto el sentido de la desigualdad se mantiene)
Si multiplicamos o dividimos los dos miembros de una desigualdad por un mismo número positivo, resulta otra del mismo sentido.
Ejemplo:
5x + 4 > 6
3(5x + 4) > 3(6)
(Ambos lados lo estamos multiplicando por 3)
15x + 12 > 18
(El sentido de la desigualdad se mantiene)
Si multiplicamos o dividimos los dos miembros de una desigualdad por un mismo número negativo, resulta otra de sentido contrario.
Ejemplo:
5x + 4 > 6
-3(5x + 4) > -3(6)
(Ambos lados lo estamos multiplicando por -3)
-15x -12 12 < -18
(El sentido de la desigualdad cambia)
Conjunto Solución
La solución de una desigualdad es el conjunto de todos los valores de la incógnita que la satisface. Resolver una desigualdad es hallar su conjunto solución, valiéndonos de las reglas utilizadas en la resolución de ecuaciones.
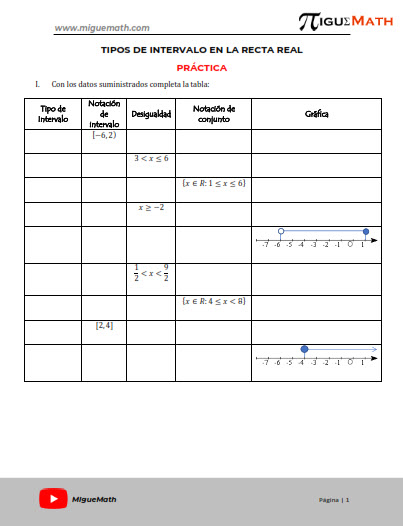
Intervalos, gráficas y límites
Un intervalo se define como un subconjunto de los números reales en el que está comprendido, entre dos números cualesquiera, a y b ∈ R; es decir, es un subconjunto de la recta numérica. Cuando sea, se definirán los siguientes tipos de intervalos en la recta real:
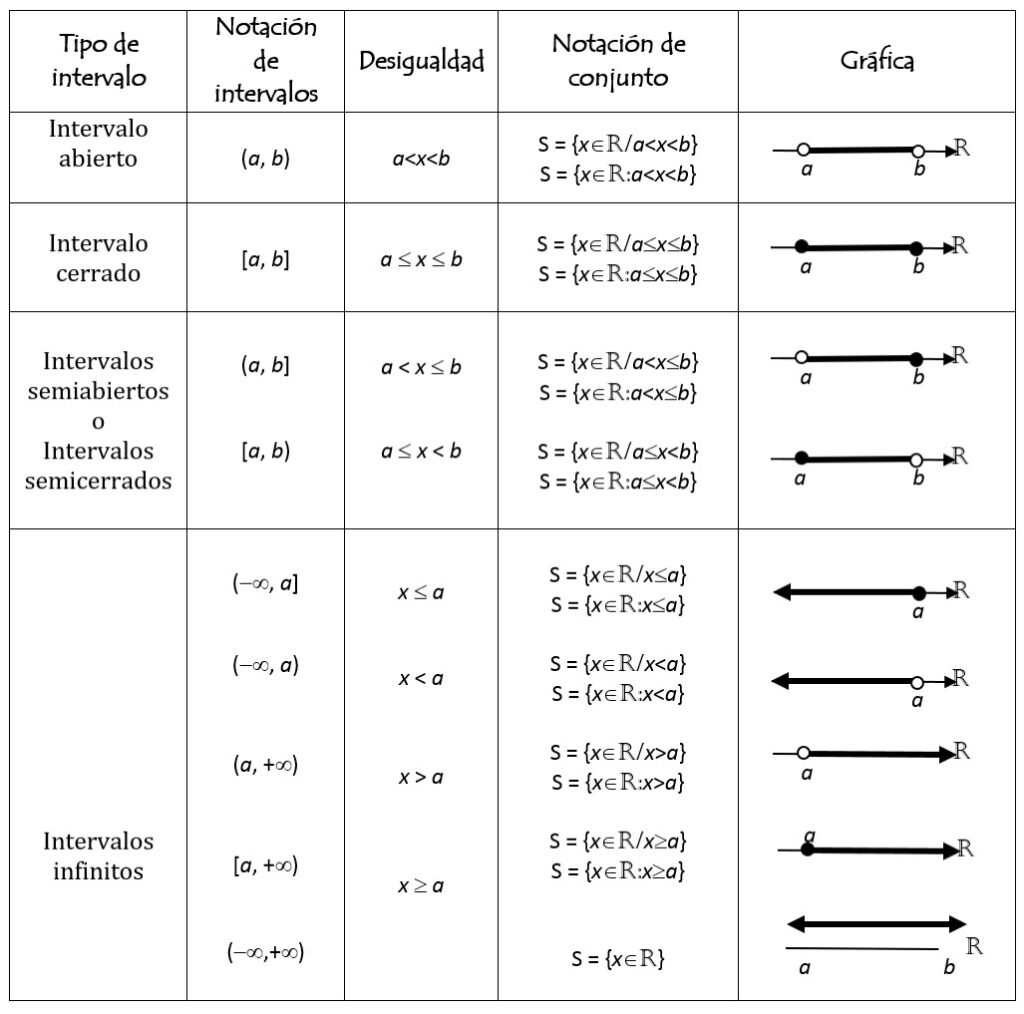
El símbolo ∞, significa infinito, a +∞ se le denomina “más infinito”, y a -∞ se le llama “menos infinito”. No debemos confundir el infinito con un número real, pues el infinito es un símbolo matemático y no obedece a las propiedades de los números. Es decir, no podemos interpretar los infinitos como si fuesen números reales.
Aprende más sobre este tema aquí:
- ¿Cómo graficar una desigualdad?